Аннуитет. Расчёт в EXCEL погашение основной суммы долга
2 февраля 2015 г.
- Группы статей
- Расчет кредитов и вкладов
- Аннуитет
Рассчитаем в MS EXCEL остаток основной суммы долга, который требуется погасить после заданного количества периодов. Выплата кредита производится равными ежемесячными платежами (аннуитетная схема). Процентная ставка и величина платежа - известны, начисление процентов за пользование кредитом – также ежемесячное.
Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат. В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа) показано как рассчитать величину регулярной суммы для погашения кредита или ссуды. В данной статье научимся вычислять остаток основной суммы долга, который требуется погасить после заданного количества периодов (а также сумму основного долга, которая была выплачена в промежутке между двумя периодами).
Вычисление остатка суммы основного долга (при БС=0, тип=0)
Пусть был взят кредит в размере 100 000руб. на 10 лет под ставку 9%. Кредит должен гаситься ежемесячными равными платежами (в конце периода). Требуется вычислить сумму основного долга, которая будет выплачена в первом месяце третьего года выплат. Решение простое – используйте функцию ОСПЛТ(): =ОСПЛТ(9%/12;25;10*12;100000) Ставка за период (ставка): 9%/12 Номер периода (первый месяц третьего года выплат): 25=2*12+1 Всего периодов (кпер): 10*12 Кредит: 100000 Ответ: Сумма основного долга, которая будет выплачена в первом месяце третьего года выплат: -618,26руб.
Теперь выполним те же вычисления, только осмысленно, т.е. понимая, суть расчета.
- Вычислим ежемесячный платеж, используя формулу Приведенной стоимости . Обозначим сумму кредита как ПС, ежемесячный платеж как ПЛТ: ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Отсюда, ПМТ=ПС* ставка /(1-(1+ставка)^-кпер)=1266,76 (правильность расчета можно проверить с помощью ПЛТ() – см. файл примера, лист Задача ). ПЛТ() вернет -1266,76. Знак минус указывает на различные направления денежных потоков + (из банка сумма кредита), - (в банк ежемесячные платежи). Формула приведенной стоимости является следствием того, что сумма долей ежемесячных платежей, идущих на погашение основной суммы долга, должна быть равна сумме кредита.
Выведем формулу:
- Доля платежа, которая идет на погашение основной суммы долга в 1-й период =ПМТ-ПС*ставка, а с учетом знаков =-ПМТ-ПС*ставка (чтобы сумма долей была того же знака, что и ПС). Обозначим эту долю как ПС1. ПС*ставка – это сумма процентов, уплаченная за пользование кредитом в первый период.
- Доля платежа, которая идет на погашение основной суммы долга в 2-й период =-ПМТ-(ПС-ПС1)*ставка=-ПМТ-(ПС +ПМТ+ПС*ставка) *ставка=(-ПМТ-ПС*ставка)*(1+ставка)=ПС1*(1+ставка). Обозначим эту долю как ПС2. ПС-ПС1 – это остаток суммы долга в конце второго периода.
- Доля платежа, которая идет на погашение основной суммы долга в 3-й период =-ПМТ-(ПС-ПС1-ПС2)*ставка=-ПМТ-(ПС-ПС1)*ставка+ПС2*ставка =ПС2+ПС2*ставка= ПС2*(1+ставка) =ПС1*(1+ставка)^2
- Очевидно, что доля платежа, которая идет на погашение основной суммы долга в последний период (кпер)= ПС1*(1+ставка)^ кпер =-(ПМТ+ПС*ставка) *(1+ставка)^ кпер
- Чтобы погасить кредит полностью, необходимо, чтобы сумма долей, идущих на погашение кредита, была равна сумме кредита, т.е. =-(ПМТ+ПС*ставка)*(1-(1+ставка)^ кпер)/ставка=ПС. Эта формула получена как сумма членов геометрической прогрессии: первый член =-(ПМТ+ПС*ставка), знаменатель =(1+ставка).
- Решая нехитрое уравнение, полученное на предыдущем шаге, получим, что ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Это и есть формула приведенной стоимости (при БС=0 и платежах, осуществляемых в конце периода (тип=0)).
- Вычислим сумму основного долга, которую нужно будет выплатить начиная с 25-го месяца (т.е. в начиная с 25 и заканчивая 120 периодом). Сделаем это используя формулу приведенной стоимости ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Теперь ПМТ нам известно, ПС – это искомая сумма основного долга, которую нужно будет выплатить, начиная с 25-го месяца, т.е. за 96 периодов (120-24=кпер). ПС=86466,91 Правильность расчета можно проверить с помощью ОБЩДОХОД() .
- Вычислим сумму процентов, которые будут выплачены в 25-й месяц: 86466,91*ставка=648,50 Правильность расчета можно проверить с помощью ПРПЛТ() .
- Наконец, т.к. каждый платеж содержит сумму, идущую в оплату основной суммы долга и начисленные за период проценты, то Сумму основного долга, которая будет выплачена в первом месяце третьего года выплат получим как: ПМТ-648,50=618,26
Как видим, сумма совпадает результатом ОСПЛТ() , вычисленную ранее (с точностью до знака).
Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами
Данные расчеты можно сделать несколькими разными способами (см. файл примера ).
Способ 1. Функция ОБЩДОХОД() Функция ОБЩДОХОД(ставка; кол_пер; нз; нач_период; кон_период; тип) возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами ( нач_период и кон_период ).
Примечание . Английская версия функции: CUMPRINC(rate, nper, pv, start_period, end_period, type) returns the CUMulative PRincipal paid for an investment period with a Constant interest rate.
Аргументы функции: Ставка - обязательный аргумент. Процентная ставка за период. Кол_пер - обязательный аргумент (кол_пер – это аргумент кпер в других функциях аннуитета, например в ПЛТ()). Общее количество периодов выплат. Нз - обязательный аргумент (нз – это аргумент пс в других функциях аннуитета, например в ПЛТ()). Начальное значение (чаще всего - сумма кредита). Нач_период - обязательный аргумент. Номер первого периода, включенного в вычисления. Нумерация периодов выплат начинается с 1. Кон_период - обязательный аргумент. Номер последнего периода, включенного в вычисления. Тип - обязательный аргумент, определяющий время платежа. Для аннуитета постнумерандо Тип=0, для пренумерандо Тип=1.
Примечание . Убедитесь, что аргумент "Ставка" соответствуют ставке за период (период не обязательно = году). Например, при ежемесячных выплатах по 4-х летнему займу из расчета 12 процентов годовых используйте значение 12%/12 для аргумента "Ставка". Аргумент "Кол_пер" будет равен 4*12. При ежегодных платежах по тому же займу используйте значение 12% для аргумента "ставка" и 4 — для аргумента "Кол_пер". При ежеквартальных платежах по тому же займу используйте значение 12%/4 для аргумента "ставка" и 4*4 — для аргумента "Кол_пер". Примечание . Функция ОБЩДОХОД() возвращает значение ошибки #ЧИСЛО! если "Ставка" ≤ 0, "кол_пер" ≤ 0 или "нз" ≤ 0, "нач_период" < 1, "кон_период" < 1 "нач_период" > "кон_период" "тип" является любым числом, отличным от 0 и 1 Примечание . Функция ОБЩДОХОД() возвращает значение ошибки #ЗНАЧ! если для "тип" использованы значения ЛОЖЬ или ИСТИНА.
Альтернативная формула
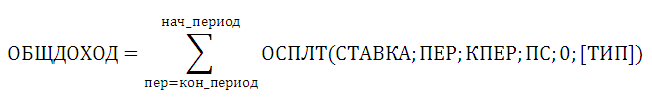
Из анализа альтернативной формулы ясно, что функция ОБЩДОХОД() может использоваться, только если БС=0, т.е. когда предполагается, что по прошествии количества периодов "Кол_пер" займ полностью погашается. Это ограничение можно обойти, записав выражение =ОБЩДОХОД(ставка; кол_пер; нз+БС; нач_период; кон_период; тип)+(нач_период=1)*тип*БС* ставка /(1+ ставка)
Способ 2. Функция ОСПЛТ()
Функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) используется для вычисления регулярных сумм идущих на погашение основной суммы долга практически с теми же аргументами, что и ПЛТ() .
Примечание . Английский вариант функции: PPMT(rate, per, nper, pv, [fv], [type]), т.е. Principal Payment – платеж основной части долга.
Чтобы вычислить сумму основного долга, которая была выплачена в промежутке между двумя периодами, нужно использовать не одну, а несколько функций ОСПЛТ() . Например, вычислим сумму долга, выплаченную в 3-м и 4-м периоде: =ОСПЛТ(ставка; 3; кпер; пс; [бс]; [тип])+ОСПЛТ(ставка; 4; кпер; пс; [бс]; [тип])
Чтобы вычислить сумму основного долга, которая была выплачена в промежутке между двумя произвольными периодами нач_период и кон_период используйте формулу: =СУММПРОИЗВ(ОСПЛТ(ставка;СТРОКА(ДВССЫЛ(нач_период&":"&кон_период)); кпер; пс; [бс]; [тип]))
Выражение СТРОКА(ДВССЫЛ(нач_период&":"&кон_период)) создает массив последовательных чисел , например 2:3:4:5 (если нач_период=2 и кон_период=5). Функция СУММПРОИЗВ() суммирует результаты ОСПЛТ() , т.е. вышеуказанная формула эквивалентна формуле: =ОСПЛТ(ставка; 2; кпер; пс; [бс]; [тип])+ОСПЛТ(ставка; 3; кпер; пс; [бс]; [тип]) + ОСПЛТ(ставка; 4; кпер; пс; [бс]; [тип])+ОСПЛТ(ставка; 5; кпер; пс; [бс]; [тип])
Способ 3. Вычисление суммы основного долга через Будущую стоимость
Функция БС(ставка; кпер; плт; [пс]; [тип]) возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки. Подробнее см. статью Аннуитет. Определяем в MS EXCEL Будущую Стоимость . Чтобы вычислить сумму основного долга, которая была выплачена в промежутке между двумя произвольными периодами нач_период и кон_период используйте формулу:
=- БС(ставка; кон_период; плт; [пс]; [тип]) /(1+тип *ставка) + БС(ставка; нач_период-1; плт; [пс]; [тип]) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)
В файле примера также приведена эквивалентная формула без использования функции БС() .
Способ 4. Вычисление суммы основного долга через Приведенную стоимость
Функция ПС(ставка; кпер; плт; [бс]; [тип]) возвращает приведенную (к текущему моменту) стоимость инвестиций. Подробнее см. статью Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость . Чтобы вычислить сумму основного долга, которая была выплачена в промежутке между двумя произвольными периодами нач_период и кон_период используйте формулу:
=ПС(ставка; кпер-кон_период; плт; [бс]; [тип]) /(1+тип *ставка) - ПС(ставка; кпер-нач_период+1; плт; [пс]; [тип]) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)
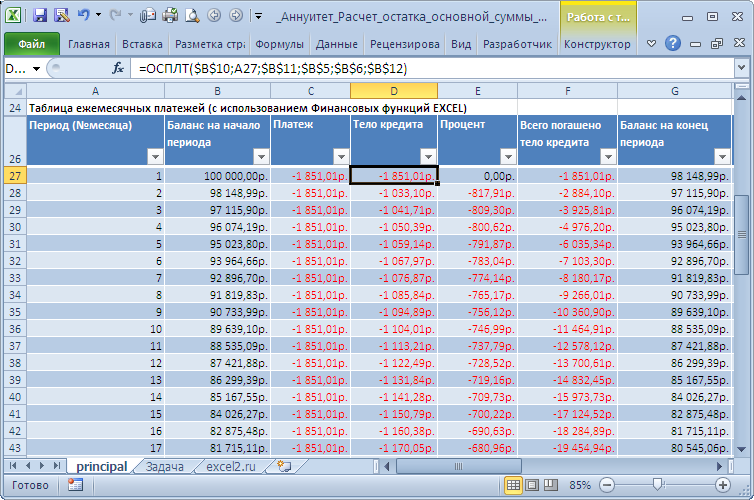
В файле примера также приведена эквивалентная формула без использования функции ПС() . Чтобы убедиться в идентичности вышеуказанных способов, в файле примера приведен график платежей, рассчитанный на основе функции ОСПЛТ() .
Комментарии